Control of jump linear systems

  We are given a linear system

where A is and B is . The scalar parameter r(t) is a continuous-time Markov process taking values in a finite set .

The transition probabilities of the process r are defined by a ``transition matrix'' , where 's are the transition probability rates from the i-th mode to the j-th. Such systems, referred to as ``jump linear systems'', can be used to model linear systems subject to failures.

We seek a state-feedback control law such that the resulting closed-loop system is mean-square stable. That is, for every initial condition x(0), the resulting trajectory of the closed-loop system satisfies .

The control law we look for is a mode-dependent linear state-feedback, i.e. it has the form u(t) = K(r(t))x(t); K(i)'s are matrices (the unknowns of our control problem).

It can be shown that this problem has a solution if and only if there exist matrices , and matrices , such that

and

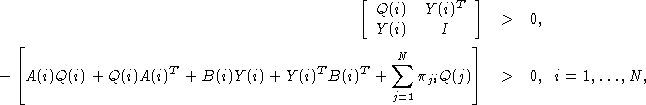
If such matrices exist, a stabilizing state-feedback is given by , .

In the above problem, the data matrices are , and the transition matrix . The unknown matrices are Q(i)'s (which are symmetric matrices) and Y(i)'s (which are matrices). In this case, both the number of the data matrices and that of the unknown matrices are a-priori unknown.

The above problem is obviously a problem. In this case, we can let XLIST be a list of two lists: one representing the Q's and the other, the Y's.

The evaluation function required for invoking lmisolver can be constructed as follows:

 function [LME,LMI,OBJ]=jump_sf_eval(XLIST)
 [Q,Y]=XLIST(:)
 N=size(A); [n,nu]=size(B(1))
 LME=list(); LMI1=list(); LMI2=list()
 tr=0
 for i=1:N
    tr=tr+trace(Q(i))
    LME(i)=Q(i)-Q(i)'
    LMI1(i)=[Q(i),Y(i)';Y(i),eye(nu,nu)]
    SUM=zeros(n,n)
    for j=1:N
      SUM=SUM+PI(j,i)*Q(j)
    end
    LMI2(i)= A(i)*Q(i)+Q(i)*A(i)'+B(i)*Y(i)+Y(i)'*B(i)'+SUM
 end
 LMI=list(LMI1,LMI2)
 LME(N+1)=tr-1
 OBJ=[]

Note that LMI is also a list of lists containing the values of the LMI matrices. This is just a matter of convenience.

Now, we can solve the problem in Scilab as follows (assuming lists A and B, and matrix PI have already been defined).

First we should initialize Q and Y.

--> N=size(A);  [n,nu]=size(B(1)); Q_init=list(); Y_init=list();
--> for i=1:N, Q_init(i)=zeros(n,n);Y_init(i)=zeros(nu,n);end

Then, we can use lmisolver as follows:

--> XLIST0=list(Q_init,Y_init)
--> XLISTF=lmisolver(XLIST0,jump_sf_eval)
--> [Q,Y]=XLISTF(:);

The above commands can be encapsulated in a solver function, say jump_sf, in which case we simply need to type:

--> [Q,Y]=jump_sf(A,B,PI)

to obtain the solution.