


This R package is a wrapper of the C++ library epiworld. It provides a general framework for modeling disease transmission using agent-based models. Some of the main features include:
From the package’s description:
A flexible framework for Agent-Based Models (ABM), the epiworldR package provides methods for prototyping disease outbreaks and transmission models using a C++ backend, making it very fast. It supports multiple epidemiological models, including the Susceptible-Infected-Susceptible (SIS), Susceptible-Infected-Removed (SIR), Susceptible-Exposed-Infected-Removed (SEIR), and others, involving arbitrary mitigation policies and multiple-disease models. Users can specify infectiousness/susceptibility rates as a function of agents’ features, providing great complexity for the model dynamics. Furthermore, epiworldR is ideal for simulation studies featuring large populations.
Current available models:
ModelDiagramModelDiffNetModelMeaslesQuarantineModelSEIRModelSEIRCONNModelSEIRDModelSEIRDCONNModelSEIRMixingModelSIRModelSIRCONNModelSIRDModelSIRDCONNModelSIRLogitModelSIRMixingModelSISModelSISDModelSURVYou can install the development version of epiworldR from GitHub with:
devtools::install_github("UofUEpiBio/epiworldR")Or from CRAN
install.packages("epiworldR")This R package includes several popular epidemiological models, including SIS, SIR, and SEIR using either a fully connected graph (similar to a compartmental model) or a user-defined network.
This Susceptible-Infected-Recovered model features a population of 100,000 agents simulated in a small-world network. Each agent is connected to ten other agents. One percent of the population has the virus, with a 70% chance of transmission. Infected individuals recover at a 0.3 rate:
library(epiworldR)
#> Thank you for using epiworldR! Please consider citing it in your work.
#> You can find the citation information by running
#> citation("epiworldR")
# Creating a SIR model
sir <- ModelSIR(
name = "COVID-19",
prevalence = .01,
transmission_rate = .7,
recovery = .3
) |>
# Adding a Small world population
agents_smallworld(n = 100000, k = 10, d = FALSE, p = .01) |>
# Running the model for 50 days
run(ndays = 50, seed = 1912)
#> _________________________________________________________________________
#> |Running the model...
#> |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
sir
#> ________________________________________________________________________________
#> Susceptible-Infected-Recovered (SIR)
#> It features 100000 agents, 1 virus(es), and 0 tool(s).
#> The model has 3 states.
#> The final distribution is: 1209 Susceptible, 499 Infected, and 98292 Recovered.Visualizing the outputs
summary(sir)
#> ________________________________________________________________________________
#> ________________________________________________________________________________
#> SIMULATION STUDY
#>
#> Name of the model : Susceptible-Infected-Recovered (SIR)
#> Population size : 100000
#> Agents' data : (none)
#> Number of entities : 0
#> Days (duration) : 50 (of 50)
#> Number of viruses : 1
#> Last run elapsed t : 132.00ms
#> Last run speed : 37.85 million agents x day / second
#> Rewiring : off
#>
#> Global events:
#> (none)
#>
#> Virus(es):
#> - COVID-19
#>
#> Tool(s):
#> (none)
#>
#> Model parameters:
#> - Recovery rate : 0.3000
#> - Transmission rate : 0.7000
#>
#> Distribution of the population at time 50:
#> - (0) Susceptible : 99000 -> 1209
#> - (1) Infected : 1000 -> 499
#> - (2) Recovered : 0 -> 98292
#>
#> Transition Probabilities:
#> - Susceptible 0.92 0.08 -
#> - Infected - 0.70 0.30
#> - Recovered - - 1.00
plot(sir)
plot_incidence(sir)
The SEIR model is similar to the SIR model but includes an exposed state. Here, we simulate a population of 10,000 agents with a 0.01 prevalence, a 0.6 transmission rate, a 0.5 recovery rate, and 7 days-incubation period. The population is fully connected, meaning agents can transmit the disease to any other agent:
model_seirconn <- ModelSEIRCONN(
name = "COVID-19",
prevalence = 0.01,
n = 10000,
contact_rate = 10,
incubation_days = 7,
transmission_rate = 0.1,
recovery_rate = 1 / 7
) |> add_virus(
virus(
name = "COVID-19 (delta)",
prevalence = 0.01,
as_proportion = TRUE,
prob_infecting = 0.2,
recovery_rate = 0.6,
prob_death = 0.5,
incubation = 7
))
set.seed(132)
run(model_seirconn, ndays = 100)
#> _________________________________________________________________________
#> Running the model...
#> |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
summary(model_seirconn)
#> ________________________________________________________________________________
#> ________________________________________________________________________________
#> SIMULATION STUDY
#>
#> Name of the model : Susceptible-Exposed-Infected-Removed (SEIR) (connected)
#> Population size : 10000
#> Agents' data : (none)
#> Number of entities : 0
#> Days (duration) : 100 (of 100)
#> Number of viruses : 2
#> Last run elapsed t : 143.00ms
#> Last run speed : 6.98 million agents x day / second
#> Rewiring : off
#>
#> Global events:
#> - Update infected individuals (runs daily)
#>
#> Virus(es):
#> - COVID-19
#> - COVID-19 (delta)
#>
#> Tool(s):
#> (none)
#>
#> Model parameters:
#> - Avg. Incubation days : 7.0000
#> - Contact rate : 10.0000
#> - Prob. Recovery : 0.1429
#> - Prob. Transmission : 0.1000
#>
#> Distribution of the population at time 100:
#> - (0) Susceptible : 9800 -> 59
#> - (1) Exposed : 200 -> 0
#> - (2) Infected : 0 -> 0
#> - (3) Recovered : 0 -> 9941
#>
#> Transition Probabilities:
#> - Susceptible 0.95 0.05 - -
#> - Exposed - 0.86 0.14 -
#> - Infected - - 0.79 0.21
#> - Recovered - - - 1.00Computing some key statistics
plot(model_seirconn)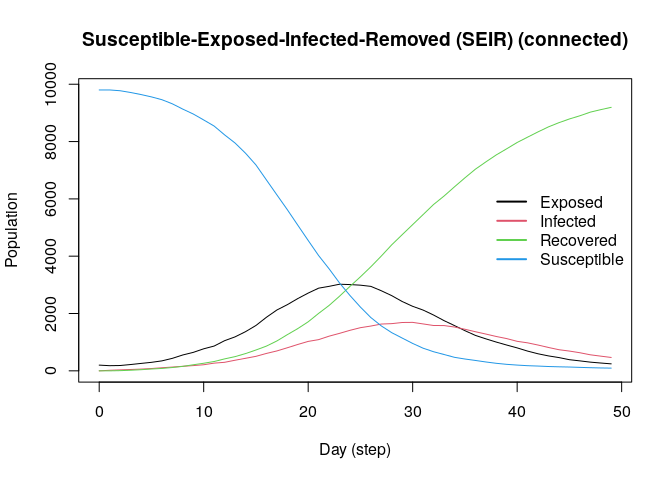
repnum <- get_reproductive_number(model_seirconn)
head(plot(repnum))
#> virus_id virus date avg n sd lb ub
#> 1 0 COVID-19 0 4.880000 100 4.159157 0 14.05
#> 2 0 COVID-19 2 5.333333 9 4.415880 1 12.60
#> 3 0 COVID-19 3 5.416667 12 3.369875 1 10.45
#> 4 0 COVID-19 4 3.480000 25 2.740438 0 9.80
#> 5 0 COVID-19 5 2.580645 31 2.790152 0 9.00
#> 6 0 COVID-19 6 3.339623 53 3.031523 0 10.40
head(plot_generation_time(model_seirconn))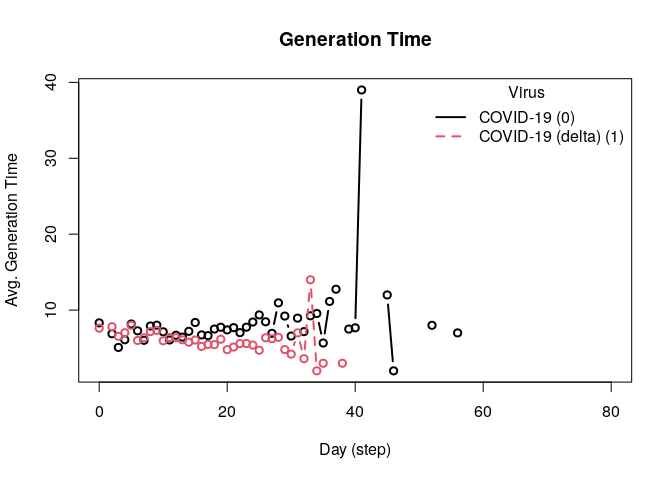
#> date avg n sd ci_lower ci_upper virus virus_id
#> 1 0 8.318681 91 5.599363 2.00 20.500 COVID-19 0
#> 2 2 6.888889 9 4.648775 2.20 14.000 COVID-19 0
#> 3 3 5.083333 12 2.503028 3.00 9.725 COVID-19 0
#> 4 4 6.095238 21 3.096849 2.00 12.500 COVID-19 0
#> 5 5 8.173913 23 6.846712 2.55 24.000 COVID-19 0
#> 6 6 7.272727 44 5.332496 2.00 19.000 COVID-19 0This model provides a more complex transmission and recovery pattern
based on agents’ features. With it, we can reflect co-morbidities that
could change the probability of infection and recovery. Here, we
simulate a population including a dataset with two features: an
intercept and a binary variable Female. The probability of
infection and recovery are functions of the intercept and the
Female variables. The following code simulates a population
of 100,000 agents in a small-world network. Each agent is connected to
eight other agents. One percent of the population has the virus, with an
80% chance of transmission. Infected individuals recover at a 0.3
rate:
# Simulating a population of 100,000 agents
set.seed(2223)
n <- 100000
# Agents' features
X <- cbind(
Intercept = 1,
Female = sample.int(2, n, replace = TRUE) - 1
)
coef_infect <- c(.1, -2, 2)
coef_recover <- rnorm(2)
# Creating the model
model_logit <- ModelSIRLogit(
"covid2",
data = X,
coefs_infect = coef_infect,
coefs_recover = coef_recover,
coef_infect_cols = 1L:ncol(X),
coef_recover_cols = 1L:ncol(X),
prob_infection = .8,
recovery_rate = .3,
prevalence = .01
)
# Adding a small-world population
agents_smallworld(model_logit, n, 8, FALSE, .01)
# Running the model
run(model_logit, 50)
#> _________________________________________________________________________
#> |Running the model...
#> |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
plot(model_logit)
# Females are supposed to be more likely to become infected
rn <- get_reproductive_number(model_logit)
(table(
X[, "Female"],
(1:n %in% rn$source)
) |> prop.table())[, 2]
#> 0 1
#> 0.13505 0.14886
# Looking into the agents
get_agents(model_logit)
#> Agents from the model "Susceptible-Infected-Removed (SIR) (logit)":
#> Agent: 0, state: Susceptible (0), Has virus: no, NTools: 0i NNeigh: 8
#> Agent: 1, state: Susceptible (0), Has virus: no, NTools: 0i NNeigh: 8
#> Agent: 2, state: Susceptible (0), Has virus: no, NTools: 0i NNeigh: 8
#> Agent: 3, state: Susceptible (0), Has virus: no, NTools: 0i NNeigh: 8
#> Agent: 4, state: Susceptible (0), Has virus: no, NTools: 0i NNeigh: 8
#> Agent: 5, state: Susceptible (0), Has virus: no, NTools: 0i NNeigh: 8
#> Agent: 6, state: Susceptible (0), Has virus: no, NTools: 0i NNeigh: 8
#> Agent: 7, state: Susceptible (0), Has virus: no, NTools: 0i NNeigh: 8
#> Agent: 8, state: Susceptible (0), Has virus: no, NTools: 0i NNeigh: 8
#> Agent: 9, state: Susceptible (0), Has virus: no, NTools: 0i NNeigh: 8
#> ... 99990 more agents ...This example shows how we can draw a transmission network from a simulation. The following code simulates a population of 500 agents in a small-world network. Each agent is connected to ten other agents. One percent of the population has the virus, with a 50% chance of transmission. Infected individuals recover at a 0.5 rate:
# Creating a SIR model
sir <- ModelSIR(
name = "COVID-19",
prevalence = .01,
transmission_rate = .5,
recovery = .5
) |>
# Adding a Small world population
agents_smallworld(n = 500, k = 10, d = FALSE, p = .01) |>
# Running the model for 50 days
run(ndays = 50, seed = 1912)
#> _________________________________________________________________________
#> |Running the model...
#> |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
# Transmission network
net <- get_transmissions(sir)
net <- subset(net, source >= 0)
# Plotting
library(epiworldR)
library(netplot)
#> Loading required package: grid
x <- igraph::graph_from_edgelist(
as.matrix(net[, 2:3]) + 1
)
nplot(x, edge.curvature = 0, edge.color = "gray", skip.vertex = TRUE)
epiworldR supports running multiple simulations using
the run_multiple function. The following code simulates 50
SIR models with 1000 agents each. Each agent is connected to ten other
agents. One percent of the population has the virus, with a 90% chance
of transmission. Infected individuals recover at a 0.1 rate. The results
are saved in a data.frame:
model_sir <- ModelSIRCONN(
name = "COVID-19",
prevalence = 0.01,
n = 1000,
contact_rate = 2,
transmission_rate = 0.9, recovery_rate = 0.1
)
# Generating a saver
saver <- make_saver("total_hist", "reproductive")
# Running and printing
# Notice the use of nthread = 2 to run the simulations in parallel
run_multiple(model_sir, ndays = 100, nsims = 50, saver = saver, nthread = 2)
#> Starting multiple runs (50) using 2 thread(s)
#> _________________________________________________________________________
#> _________________________________________________________________________
#> ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| done.
# Retrieving the results
ans <- run_multiple_get_results(model_sir)
head(ans$total_hist)
#> sim_num date nviruses state counts
#> 1 1 0 1 Susceptible 990
#> 2 1 0 1 Infected 10
#> 3 1 0 1 Recovered 0
#> 4 1 1 1 Susceptible 973
#> 5 1 1 1 Infected 27
#> 6 1 1 1 Recovered 0
head(ans$reproductive)
#> sim_num virus_id virus source source_exposure_date rt
#> 1 1 0 COVID-19 683 9 0
#> 2 1 0 COVID-19 983 8 0
#> 3 1 0 COVID-19 875 8 0
#> 4 1 0 COVID-19 801 8 0
#> 5 1 0 COVID-19 770 8 0
#> 6 1 0 COVID-19 758 8 0
plot(ans$reproductive)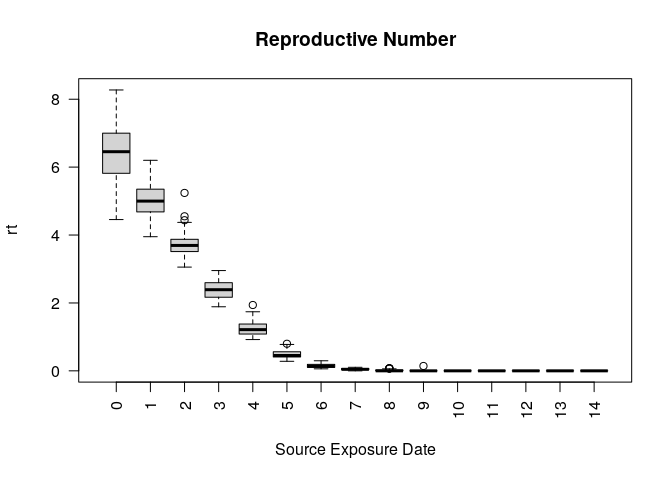
The virtual INSNA Sunbelt 2023 session can be found here: https://github.com/UofUEpiBio/epiworldR-workshop/tree/sunbelt2023-virtual
The in-person INSNA Sunbelt 2023 session can be found here: https://github.com/UofUEpiBio/epiworldR-workshop/tree/sunbetl2023-inperson
If you use epiworldR in your research, please cite it as
follows:
citation("epiworldR")
#> To cite epiworldR in publications use:
#>
#> Meyer, Derek and Vega Yon, George (2023). epiworldR: Fast Agent-Based
#> Epi Models. Journal of Open Source Software, 8(90), 5781,
#> https://doi.org/10.21105/joss.05781
#>
#> And the actual R package:
#>
#> Meyer D, Pulsipher A, Vega Yon G (2025). _epiworldR: Fast Agent-Based
#> Epi Models_. R package version 0.8.3.0,
#> <https://github.com/UofUEpiBio/epiworldR>.
#>
#> To see these entries in BibTeX format, use 'print(<citation>,
#> bibtex=TRUE)', 'toBibtex(.)', or set
#> 'options(citation.bibtex.max=999)'.Several alternatives to epiworldR exist and provide
researchers with a range of options, each with its own unique features
and strengths, enabling the exploration and analysis of infectious
disease dynamics through agent-based modeling. Below is a manually
curated table of existing alternatives, including ABM [@ABM], abmR [@abmR], cystiSim [@cystiSim], villager
[@villager], and
RNetLogo [@RNetLogo].
| Package | Multiple Viruses | Multiple Tools | Multiple Runs | Global Actions | Built-In Epi Models | Dependencies | Activity |
|---|---|---|---|---|---|---|---|
| epiworldR | yes | yes | yes | yes | yes |  |
 |
| ABM | - | - | - | yes | yes |  |
 |
| abmR | - | - | yes | - | - |  |
 |
| cystiSim | - | yes | yes | - | - |  |
 |
| villager | - | - | - | yes | - |  |
 |
| RNetLogo | - | yes | yes | yes | - |  |
 |
You may want to check out other R packages for agent-based modeling:
ABM,
abmR,
cystiSim,
villager, and
RNetLogo.
We welcome contributions to the epiworldR package! If you would like to contribute, please review our development guidelines before creating a pull request.
The epiworldR project is released with a Contributor Code of Conduct. By contributing to this project, you agree to abide by its terms.