The adept package implements ADaptive Empirical Pattern
Transformation (ADEPT) method[1] for pattern segmentation from a
time-series. ADEPT is optimized to perform fast, accurate walking
strides segmentation from high-density data collected with a wearable
accelerometer during walking. The method was validated using data
collected with sensors worn at left wrist, left hip and both ankles.
Install adept package from GitHub.
# install.packages("devtools")
devtools::install_github("martakarass/adept")We simulate a time-series x. We assume that
x is collected at a frequency of 100 Hz, there is one shape
of a pattern within x, each pattern lasts 1 second, and
there is no noise in collected data.
true.pattern <- cos(seq(0, 2 * pi, length.out = 100))
x <- c(true.pattern[1], replicate(10, true.pattern[-1]))
par(mfrow = c(1,2), cex = 1)
plot(true.pattern, type = "l", xlab = "", ylab = "", main = "Pattern")
plot(x, type = "l", xlab = "", ylab = "", main = "Time-series x")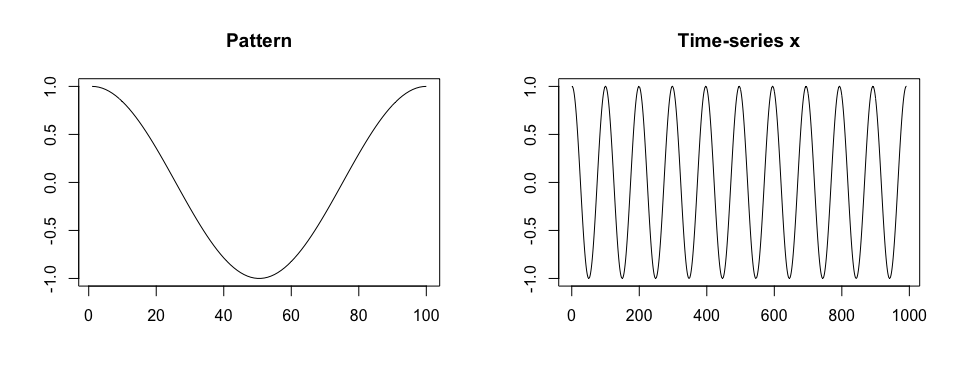
We segment pattern from data. We assume that a perfect template is
available. We use a grid of potential pattern durations of {0.9, 0.95,
1.03, 1.1} seconds; the grid is imperfect in a sense it does not contain
the duration of the true pattern used in x simulation.
library(adept)
segmentPattern(
x = x,
x.fs = 100,
template = true.pattern,
pattern.dur.seq = c(0.9, 0.95, 1.03, 1.1),
similarity.measure = "cor",
compute.template.idx = TRUE)
#> tau_i T_i sim_i template_i
#> 1 4 95 0.9987941 1
#> 2 98 103 0.9992482 1
#> 3 202 95 0.9987941 1
#> 4 296 103 0.9992482 1
#> 5 400 95 0.9987941 1
#> 6 494 103 0.9992482 1
#> 7 598 95 0.9987941 1
#> 8 692 103 0.9992482 1
#> 9 796 95 0.9987941 1
#> 10 895 95 0.9987941 1The segmentation result is a data frame, where each row describes one identified pattern occurrence:
tau_i - index of x where pattern
starts,T_i - pattern duration, expressed in x
vector length,sim_i - similarity between a template and
x,template_i - index of a template best matched to a
time-series x (here: one template was used, hence all
template_i’s equal 1).We then assume a grid of potential pattern durations which contains
the duration of the true pattern used in data simulation. A perfect
match (sim_i = 1) between a time-series x and
a template is obtained.
segmentPattern(
x = x,
x.fs = 100,
template = true.pattern,
pattern.dur.seq = c(0.9, 0.95, 1, 1.03, 1.1),
similarity.measure = "cor",
compute.template.idx = TRUE)
#> tau_i T_i sim_i template_i
#> 1 1 100 1 1
#> 2 100 100 1 1
#> 3 199 100 1 1
#> 4 298 100 1 1
#> 5 397 100 1 1
#> 6 496 100 1 1
#> 7 595 100 1 1
#> 8 694 100 1 1
#> 9 793 100 1 1
#> 10 892 100 1 1We simulate a time-series x. We assume that
x is collected at a frequency of 100 Hz, there are two
shapes of a pattern within x, patterns have various
duration, and there is no noise in collected data.
Then, we generate x2 as a noisy version of
x.
true.pattern.1 <- cos(seq(0, 2 * pi, length.out = 200))
true.pattern.2 <- true.pattern.1
true.pattern.2[70:130] <- 2 * true.pattern.2[min(70:130)] + abs(true.pattern.2[70:130])
x <- numeric()
for (vl in seq(70, 130, by = 10)){
true.pattern.1.s <- approx(
seq(0, 1, length.out = 200),
true.pattern.1, xout = seq(0, 1, length.out = vl))$y
true.pattern.2.s <- approx(
seq(0, 1, length.out = 200),
true.pattern.2, xout = seq(0, 1, length.out = vl))$y
x <- c(x, true.pattern.1.s[-1], true.pattern.2.s[-1])
if (vl == 70) x <- c(true.pattern.1.s[1], x)
}
set.seed(1)
x2 <- x + rnorm(length(x), sd = 0.5)
par(mfrow = c(1,2), cex = 1)
plot(true.pattern.1, type = "l", xlab = "", ylab = "", main = "Pattern 1")
plot(true.pattern.2, type = "l", xlab = "", ylab = "", main = "Pattern 2")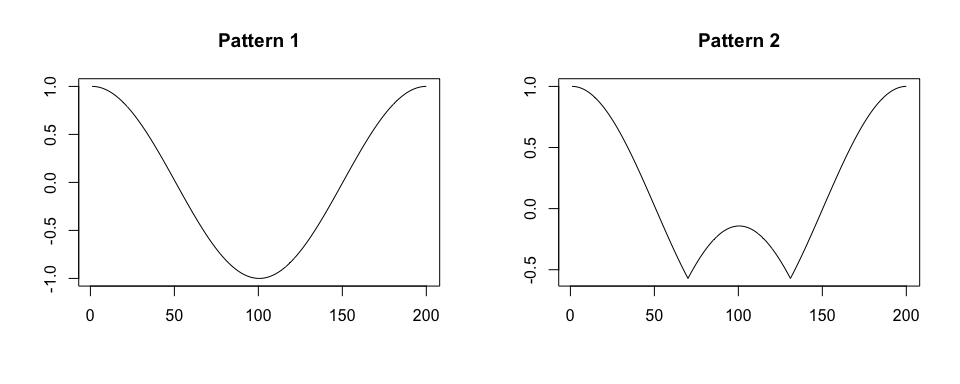
par(mfrow = c(1,1), cex = 1)
plot(x, type = "l", xlab = "", ylab = "", main = "Time-series x")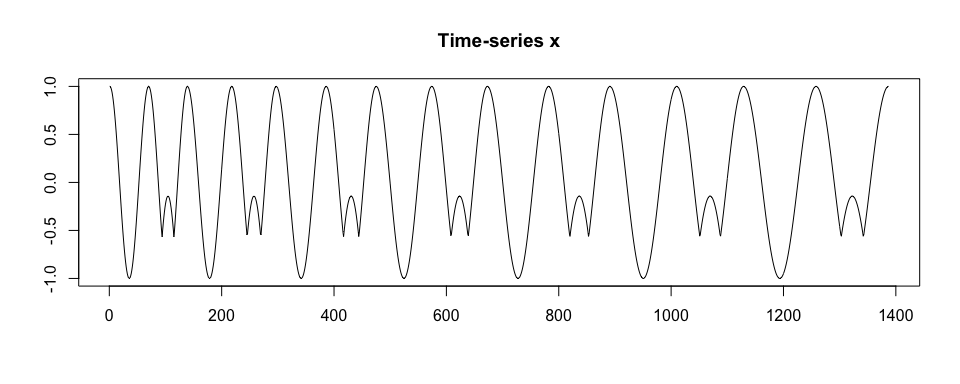
plot(x2, type = "l", xlab = "", ylab = "", main = "Time-series x2")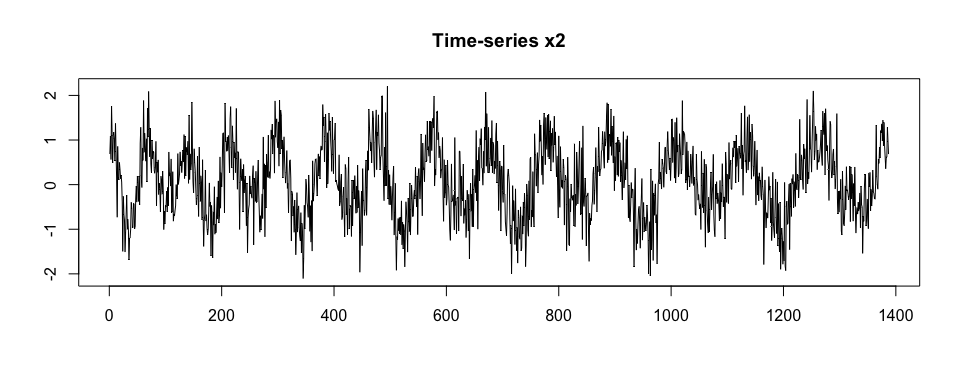
We segment x. We assume a perfect grid of potential
pattern duration, {0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3} seconds.
segmentPattern(
x = x,
x.fs = 100,
template = list(true.pattern.1, true.pattern.2),
pattern.dur.seq = seq(0.7, 1.3, by = 0.1),
similarity.measure = "cor",
compute.template.idx = TRUE)
#> tau_i T_i sim_i template_i
#> 1 1 70 1 1
#> 2 70 70 1 2
#> 3 139 80 1 1
#> 4 218 80 1 2
#> 5 297 90 1 1
#> 6 386 90 1 2
#> 7 475 100 1 1
#> 8 574 100 1 2
#> 9 673 110 1 1
#> 10 782 110 1 2
#> 11 891 120 1 1
#> 12 1010 120 1 2
#> 13 1129 130 1 1
#> 14 1258 130 1 2We segment x2.
segmentPattern(
x = x2,
x.fs = 100,
template = list(true.pattern.1, true.pattern.2),
pattern.dur.seq = seq(0.7, 1.3, by = 0.1),
similarity.measure = "cor",
compute.template.idx = TRUE)
#> tau_i T_i sim_i template_i
#> 1 1 70 0.8585451 1
#> 2 138 80 0.7624002 1
#> 3 218 80 0.7025577 2
#> 4 297 90 0.8500864 1
#> 5 390 80 0.6931671 2
#> 6 469 110 0.8286013 1
#> 7 579 90 0.6373846 2
#> 8 668 120 0.8027177 1
#> 9 787 100 0.6666713 2
#> 10 888 130 0.7894766 1
#> 11 1017 110 0.6599280 1
#> 12 1129 130 0.7938183 1
#> 13 1267 120 0.7655408 2We now use x.adept.ma.W argument to smooth
x2 before similarity matrix computation in the segmentation
procedure (see ?segmentPattern for details). We also assume
a more dense grid of potential pattern duration. We observe that
sim_i values obtained are higher than in the previous
segmentation case.
par(mfrow = c(1,1), cex = 1)
plot(windowSmooth(x = x2, x.fs = 100, W = 0.1),
type = "l", xlab = "", ylab = "", main = "Time-series x2 smoothed")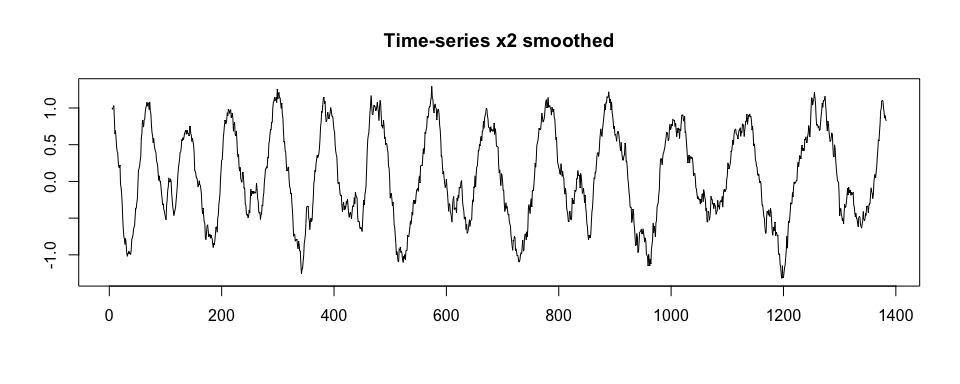
segmentPattern(
x = x2,
x.fs = 100,
template = list(true.pattern.1, true.pattern.2),
pattern.dur.seq = 70:130 * 0.01,
similarity.measure = "cor",
x.adept.ma.W = 0.1,
compute.template.idx = TRUE)
#> tau_i T_i sim_i template_i
#> 1 1 70 0.9865778 1
#> 2 70 70 0.9533684 2
#> 3 139 79 0.9683054 1
#> 4 217 80 0.9748040 2
#> 5 296 94 0.9802473 1
#> 6 391 82 0.9462213 2
#> 7 472 106 0.9855837 1
#> 8 578 93 0.9608881 2
#> 9 670 115 0.9887225 1
#> 10 784 107 0.9562694 2
#> 11 896 113 0.9734575 1
#> 12 1008 127 0.9703118 1
#> 13 1134 116 0.9606235 1
#> 14 1266 122 0.9593345 2Vignettes are available to better demonstrate package methods usage.
Vignette Introduction
to adept package introduces ADEPT algorithm and demonstrates the
usage of segmentPattern function which implements ADEPT
approach. Here, we focus on examples with simulated data.
Vignette Walking
strides segmentation with adept provides an example of segmentation
of walking strides (two consecutive steps) in sub-second accelerometry
data with adept package. The exemplary dataset is a part of
the adeptdata package. We demonstrate that ADEPT can be
used to perform automatic and precise walking stride segmentation from
data collected during a combination of running, walking and resting
exercises. We introduce how to segment data:
adeptdata
package),